The Rosenberg Self-Esteem Scale - A drosophila melanogaster of psychological assessment

I had the great chance to co-author two recent publications of Timo Gnambs, both dealing with the Rosenberg Self-Esteem Scale (RSES; Rosenberg, 1965). As a reminder, the RSES is a popular ten item self-report instrument measuring a respondent’s global self-worth and self-respect. But basically both papers are not about the RSES per se, rather they are applications of two recently introduced powerful and flexible extensions of the Structural Equation Modeling (SEM) Framework: Meta-Analytic Structural Equation Modeling (MASEM) and Local Weighted Structural Equation Modeling (LSEM), which will be described in more detail later on.

As a preliminary notion, a great deal of the psychological assessment literature is intrigued (or obsessed) with the question of dimensionality of a psychological measure. If you take a look at the table of content of any assessment journal (e.g., Assessment, European Journal of Psychological Assessment, Psychological Assessment), you’ll find several publications dealing with the factor structure of a psychological instrument. That’s in the nature of things. Or, as Reise, Moore, and Haviland (2010) formulated:

The application of psychological measures often results in item response data that arguably are consistent with both unidimensional (a single common factor) and multidimensional latent structures (typically caused by parcels of items that tap similar content domains). As such, structural ambiguity leads to seemingly endless “confirmatory” factor analytic studies in which the research question is whether scale scores can be interpreted as reflecting variation on a single trait.

To break this vicious circle, Reise et al. (2010) re-discovered the bi-factor model. Besides the appropriate way of modeling, another issue is that factors moderating the structure are left out.

Meta-Analytic Structural Equation Modeling (MASEM)

MASEM is the integration of two techniques—Meta-Analysis and Structural Equation Modeling—that have a long-standing tradition, but with limited exchange between both disciplines. There are more or less technically written primers on MASEM (Cheung, 2015a, Cheung & Chang, 2005, Cheung & Cheung, 2016) and of course the books by Mike Cheung (2015b) and Suzanne Jak (2015), but the basic idea is rather simple. MASEM is a two-stage approach: In a first step, the correlation coefficients have to be extracted from primary studies, which are meta-analytically combined into a pooled correlation matrix. Often, this correlation is simply taken as input for a structural question model, but this approach is flawed in several ways (see Cheung & Chang, 2005 for a full account). For example, often the combined correlation matrix is equated with a variance-covariance, which leads to biased fit statistics and parameter estimates (Cudeck, 1989). Another issue concerns determination of the sample size, which is usually done by calculating the mean of the individual sample sizes. However, correlations that are based on more studies are estimated with more precision and should have a larger impact. The two-stage MASEM approach described by Cheung tackle these issue.

I think there are three assets of this study worth mentioning:

  1. MASEM was conducted on item-level rather than construct-level. This is raising the examination of measures’ dimensionality to a completely new level.
  2. One might ask how relevant MASEM really is if correlation matrices are the initial source of input. But here comes an ingenious trick into play: Gnambs and Staufenbiel (2016) recently introduced a method to reproduce the item-level correlation by using the factor pattern matrices! Thus, in our study on the dimensionality of the RSES, only 10 papers reported the correlation matrix, we had 26 raw data sets to calculate the correlation matrix ourselves, but in 77 cases we used the factor pattern matrices.
  3. In accordance with Commitment to Research Transparency and Open Science which I signed a year ago, the coding material, the data, and all syntax necessary to reproduce the results are stored in an online repository on the Open Science Framework https://osf.io/uwfsp/

Reference. Gnambs, T., Scharl, A., & Schroeders, U. (2018). The structure of the Rosenberg Self-Esteem Scale: A cross-cultural meta-analysis. Zeitschrift für Psychologie, 226, 14–29. doi:10.1027/2151-2604/a000317

Abstract. The Rosenberg Self-Esteem Scale (RSES; Rosenberg, 1965) intends to measure a single dominant factor representing global self-esteem. However, several studies have identified some form of multidimensionality for the RSES. Therefore, we examined the factor structure of the RSES with a fixed-effects meta-analytic structural equation modeling approach including 113 independent samples (N = 140,671). A confirmatory bifactor model with specific factors for positively and negatively worded items and a general self-esteem factor fitted best. However, the general factor captured most of the explained common variance in the RSES, whereas the specific factors accounted for less than 15%. The general factor loadings were invariant across samples from the United States and other highly individualistic countries, but lower for less individualistic countries. Thus, although the RSES essentially represents a unidimensional scale, cross-cultural comparisons might not be justified because the cultural background of the respondents affects the interpretation of the items.

Local Weighted Structural Equation Modeling (LSEM)

Local Weighted Structural Equation Modeling (LSEM) is a recently development SEM technique (Hildebrandt et al., 2009; Hildebrandt et al., 2016) to study invariance of model parameters over a continuous context variable such as age. Frequently, the influence of context variables on parameters in a SEM is studied by introducing a categorical moderator variable and by applying multiple-group mean and covariance structure (MGMCS) analyses. In MGMCS, certain measurement parameters are fixed to be equal across groups to test for different forms of measurement invariance. LSEM, however, allows studying variance–covariance structures depending on a continuous context variable.

There are several conceptual and statistical issues in categorizing context variables that are continuous in nature (see also MacCallum, Zhang, Preacher, & Rucker, 2002). First, in the framework of MGMCS, building subgroups increases the risk of overlooking nonlinear trends and interaction effects (Hildebrandt et al., 2016). Second, categorization leads to a loss in information on individual differences within a given group. When observations that differ across the range of a continuous variable are grouped, variation within those groups cannot be detected. Third, setting cutoffs and cutting a distribution of a moderator into several parts is frequently arbitrary. Thus, neither the number of groups nor the ranges of the context variables are unique. Critically, the selected ranges can influence the results (Hildebrandt et al., 2009; MacCallum et al., 2002). In summary, from a psychometric viewpoint there are several advantages in using LSEM to study measurement invariance depending on a continuous moderator variable.

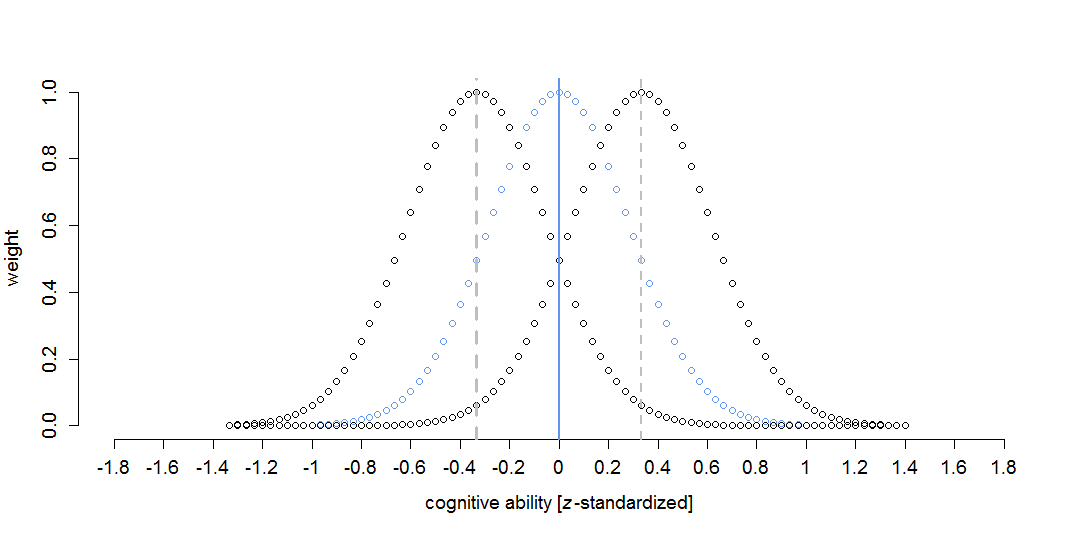
In principle, LSEMs are traditional SEMs that weight observations around focal points (i.e., specific values of the continuous moderator variable) with a kernel function. The core idea is that observations near the focal point provide more information for the corresponding SEM than more distant observations, which is also depicted in the figure. Observations exactly at the focal point receive a weight of 1; observations with moderator values higher or lower than the focal point receive smaller weights. For example, if the difference between the focal point and moderator is |1/3|, the weight is about .50 (see the gray dashed lines).

Again, I want to mention two highlights of the paper:

  1. Since the introduction of LSEM by Hildebrandt, Robitzsch, and Wilhelm (2009), the method has been successfully applied in several distinct fields: For the study of gene-environment interactions by Briley, Bates, Harden, and Tucker-Drob (2015), investigating age-related changes in face cognition abilities across adult life span and childhood age (Hildebrandt, Sommer, Herzmann, & Wilhelm, 2010; Hildebrandt, Wilhelm, Herzmann, & Sommer, 2013), and for the examination of age-related differentiation-dedifferentiation of cognitive abilities (Hülür, Wilhelm, & Robitzsch, 2011; Schroeders, Schipolowski, & Wilhelm, 2015). The current paper is an application of LSEM to reading ability as a moderator. And I wondered why hasn’t someone before thought of using ability as moderator, until Timo came up with this smart idea? I guess because the outcome in all previous studies was some kind of ability construct (e.g., face cognition or intelligence) and if you have substantial correlations between the outcome and a moderator you ran in some substantial problems, which is outlined by Hildebrandt et al. (2016). But the correlation between self-esteem and reading ability, vocabulary, and reasoning is close to zero.
  2. The variance–covariance matrix between the 10 items of the RSES is provided in the supplemental material (Table S1). Moreover, researchers accepting the respective legal and confidentially agreement can download the complete data set analyzed in this study (http://www.neps-data.de). Also all R scripts (R Core Team, 2017) are provided in an online repository of the Open Science Framework https://osf.io/bkzjy. Thus, it is another paper Open Data and Open Material. 🙂

Reference. Gnambs, T. & Schroeders, U. (2017). Cognitive abilities explain wording effects in the Rosenberg Self-Esteem Scale. Assessment. Advance online publication. doi:10.1177/1073191117746503

Abstract. There is consensus that the 10 items of the Rosenberg Self-Esteem Scale (RSES) reflect wording effects resulting from positively and negatively keyed items. The present study examined the effects of cognitive abilities on the factor structure of the RSES with a novel, nonparametric latent variable technique called local structural equation models. In a nationally representative German large-scale assessment including 12,437 students competing measurement models for the RSES were compared: a bifactor model with a common factor and a specific factor for all negatively worded items had an optimal fit. Local structural equation models showed that the unidimensionality of the scale increased with higher levels of reading competence and reasoning, while the proportion of variance attributed to the negatively keyed items declined. Wording effects on the factor structure of the RSES seem to represent a response style artifact associated with cognitive abilities.

And what about the structure of the RSES?

In both studies, we argue for a bifactor model with a common RSES factor and a specific factor for all negatively worded items. Some more complex model (i.e., additional residual correlation between two of the positively worded items 3 and 4) had a better fit, but was totally data-driven. However, the model with the nested method factor for the negatively worded items is perfectly in line with the previous literature (e.g., Motl & DiStefano, 2002).

References

#assessment #open science #LSEM #MASEM