Example 2: Test Validation With Randomized Item Sampling
Objective
The example describes the validation of a newly developed computerized personality test with a forced-choice response format comparable to the Eysenck Personality Inventory (e.g., “Do you prefer reading to going out?”, yes/no). The test is assumed to contain 30 items. A random sample of the personality test items is drawn and the correlation with an external metric criterion (e.g., number of Facebook friends) is estimated. The parameter of interest is the standard error of the correlation between the latent trait and the criterion, which depends on both the sample size and the amount of missingness.
I. Determining the data generation for the complete dataset
1. Number and distribution of factors (unidimensional vs. multidimensional)
2. Number of items and item parameters (discriminations, difficulties)
3. Item type (dichotomous, polytomous)
The true item parameters for the 30 dichotomous items are generated.
# Clear work space and load necessary packages
rm(list = ls())
library(tidyverse) # General data handling and manipulation
library(TAM) # Item response theory modeling
library(mirt) # Simulate data from a multivariate normal distribution
library(MASS) # Simulate data from a multivariate normal distribution
# Set the seed for random number generation to ensure reproducibility
set.seed(2024)
# Number of items
n_items <- 30
# Discrimination parameters (a_i) are randomly drawn from a log-normal
# distribution, as it reflects the natural variation and positive skew
# typically observed in empirical data.
a_i <- rlnorm(n_items,.2,.3)
# Difficulty parameters (b_i) are randomly drawn from a normal distribution
b_i <- rnorm(n_items, 0, 1)
The function generate_mv_data uses mirt::simdata to simulate dichotomous data given the item discriminations ($a$), the item difficulties ($b$), and the trait distribution ($\theta$). In contrast to the first example, individuals’ abilities ($\theta$) are generated according to a multivariate normal distribution with a correlation of $\rho = 0.5$ between the latent trait and the criterion.
Note that the mirt package uses slope-intercept parameterization, so the item difficulty parameters ($b$) must be transformed into the item intercepts $d_i = -a_i*b_i$. The transformation between the traditional IRT parameters (item discrimination and item difficulty) and the slope-intercept parameters can also be done with mirt::traditional2mirt.
# Simulate dichotomous item responses based on the generated theta values
# - 'a' denotes the item discriminations
# - 'b' denotes the item difficulties
# - 'theta' denotes the univariate trait distribution
generate_mv_data <- function(a, b, theta) {
resp <-
simdata(a = a, d = -a*b, Theta = theta[, 1], itemtype = "dich") %>%
as.data.frame()
return(resp)
}
II. Defining the test design and the process of missing values
4. Pattern of missingness (e.g., type of missingness, linking design)
5. Amount of missing data
The items of the computer-administered personality test are randomly drawn from a larger item pool. This kind of missingness, where the probability of missing data on a variable is independent of both observed and unobserved data, is known as Missing Completely At Random (MCAR). The function data_MCAR_design uses the complete simulated data and deletes observations under the assumption of MCAR.
# Induce missingness completely at random (MCAR) to the complete simulated data set
# - 'resp' denotes the complete data set
# - 'miss_rates' denotes the amount of missingness [0;1]
data_MCAR_design <- function(resp, miss_rates = 0) {
resp <- t(apply(resp, 1, function(row) {
row[sample(seq_along(row), length(row) * miss_rates)] <- NA;
return(row)
}))
return(resp)
}
III. Selecting the IRT model and the parameter of interest
6. Underlying IRT model (e.g., 1PL, 2PL)
7. IRT modeling software and estimation method
8. Parameters to extract
The tam.mml.2pl function from the TAM package is used to estimate the two-parametric item response model (Birnbaum model) using the simulated data. The function returns the standard error of the correlation between the latent trait and the metric covariate. Note that this example uses TAM because the criterion can be included in a latent regression model, and the standard error of the regression coefficient can be extracted directly. Alternatively, a bootstrapped standard error could be obtained via mirt using the R package boot.
# Estimate item response model
# - 'resp' denotes the data set
estimate_irt <- function(resp) {
# Estimate a 2PL model using try-catch to handle errors, the 2nd dimension of 'theta'
# is included as an additional predictor variable.
mod <- tryCatch(
tam.mml.2pl(resp = resp, # 2PL model
Y = data.frame(theta[, 2]), # matrix of covariates in latent regression
verbose = FALSE),
error = function(e) NULL
)
# Calculate standard errors for the correlation if model is successfully estimated
if (!is.null(mod)) {
est <- tam.se(mod)$beta[2, 2] # Extract the standard error of the correlation
} else {
est <- NA
}
return(est)
}
IV. Setting up the Monte Carlo Simulation
9. Number of iterations
10. Sample sizes to evaluate
The Monte Carlo simulation runs n_iterations times, including the previous steps of (i) determining the data generation for the complete dataset, (ii) defining the test design and the process of missing values, (iii) selecting the IRT model and the parameter of interest. The simulation is run for different sample sizes between 200 and 700 (in increments of 50) and three different missing rates (0%, 33%, 67%).
The standard deviation of the SE of the correlation derived from 500 iterations was low ($\sigma = .0052$), also in the most demanding condition ($n$ = 200, missing rate = 67%). Combined with a specified level of accuracy ($\delta = .001$) and a significance level ($\alpha = .05$), this implies a number of required iterations of approximately 104. Therefore, we use 104 iterations for the different sample sizes and missing rates.
# Number of iterations
n_iterations <- 104
# Sample sizes (from 200 to 700, in steps of 50) and three missing rates
grid <- expand.grid(n_persons = seq(200, 700, 50),
miss_rates = c(0.67, 0.33, 0.00))
# Create data frame for results (res)
res <- data.frame()
# Check if result file already exists
if (file.exists("example_2_res.rds")) {
res <- readRDS("example_2_res.rds")
} else {
# Loop over different sample sizes and missing rate combinations
for (g in 1:nrow(grid)) {
# Nested loop, running 'n_iterations' times
for (iter in 1:n_iterations) {
# Generate a random sample with 'n_persons' from a multivariate normal distribution
# - 'mu' denotes the mean vector for the multivariate normal distribution
# - 'Sigma' denotes the covariance matrix with a correlation of 0.5 between dimensions
theta <- mvrnorm(n = grid[g, "n_persons"],
mu = c(0, 0),
Sigma = matrix(c(1, 0.5, 0.5, 1), nrow = 2))
dat <- generate_mv_data(a_i, b_i, theta) %>%
data_MCAR_design(miss_rates = grid[g, "miss_rates"])
res <- bind_rows(res,
data.frame(iteration = iter,
n_persons = grid[g, "n_persons"],
percent_miss = grid[g, "miss_rates"],
se_est = estimate_irt(dat)))
}
}
# Save the results
saveRDS(res, file = "example_2_res.rds")
}
Results
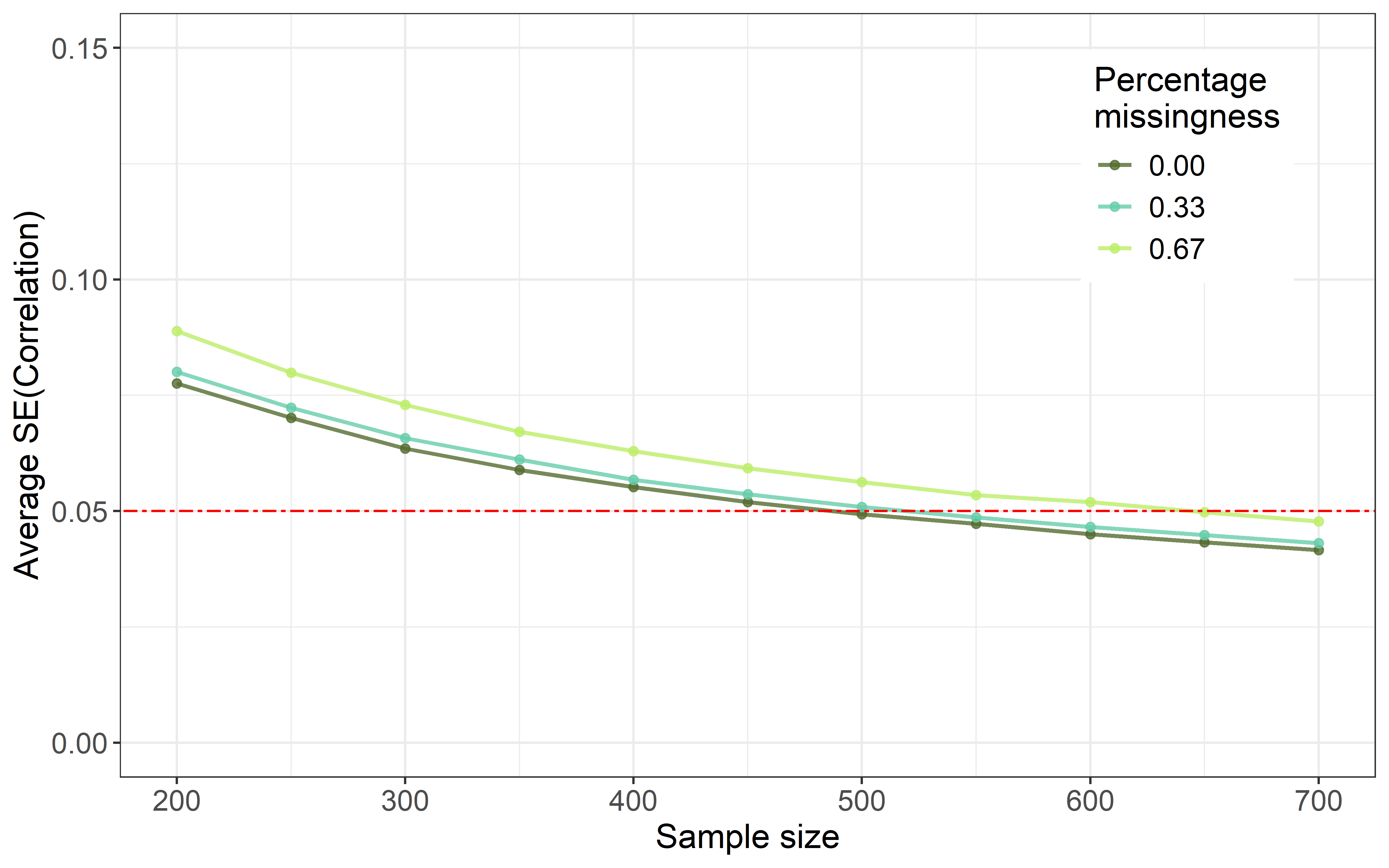
The figure shows the average standard error for the correlation between the latent trait and an external criterion as a function of sample size on one hand, and the amount of missingness on the other.
# Preparation and aggregation of results
res_plot <- res %>%
mutate(percent_miss_dec = sprintf("%.2f", percent_miss)) %>% group_by(n_persons, percent_miss_dec) %>%
summarise(
m_SE = mean(se_est^2, na.rm = TRUE)^.5, # Calculate the average SE
.groups = 'drop')
# Plot standard error of correlation
ggplot(data=res_plot, aes(x=n_persons, y = m_SE, color = factor(percent_miss_dec))) +
geom_line(linewidth = 0.8, alpha = 0.8) +
geom_point(size = 1.5, alpha = 0.8) +
geom_abline(intercept = .05, slope = 0, col="red", lty = "twodash") +
labs(
x = "Sample size",
y = "Average SE(Correlation)",
color = "Percentage\nmissingness",
linetype = "Percentage\nmissingness"
) +
scale_color_manual(values = c("0.00" = "darkolivegreen",
"0.33" = "aquamarine3",
"0.67" = "darkolivegreen2")) +
ylim(0, 0.15) +
xlim(200, 700) +
theme_bw() +
theme(
axis.title = element_text(size = 14),
axis.text = element_text(size = 12),
legend.title = element_text(size = 14),
legend.text = element_text(size = 12),
legend.position = "inside",
legend.position.inside = c(.85, .80)
)
# Documentation for transparency and reproducibility
print(sessionInfo(), locale=FALSE)