Example 1: Piloting Testing with a Linked Test Design
Objective
The example demonstrates how to determine the sample size required to estimate the item difficulties of a one-parametric item response model with a given precision. In the study, two test versions, A and B, are administered, each containing 18 items. Twelve items are unique to each test version, while six items are common to both test versions. The parameter of interest is the Mean Squared Error (MSE) of the item difficulty parameters in a one-parametric item response model.
I. Determining the data generation for the complete dataset
1. Number and distribution of factors (unidimensional vs. multidimensional)
2. Number of items and item parameters (discriminations, difficulties)
3. Item type (dichotomous, polytomous)
The true item parameters for the 30 dichotomous items are generated.
# Clear work space and load necessary packages
rm(list = ls())
library(tidyverse) # General data handling and manipulation
library(mirt) # Item response theory modeling
# Set the seed for random number generation to ensure reproducibility
set.seed(2024)
# Number of items
n_items <- 30
# Discrimination parameters are randomly drawn from a normal distribution
# with a mean of 1 and a standard deviation of 0.1 to result in parameters
# that closely conform to the 1PL while still exhibiting some misfit, that
# is the discriminations vary slightly around 1.
a_i <- rnorm(n_items, 1, 0.1)
# Difficulty parameters are equally spaced between -2 and 2 to cover the
# expected difficulty range of the latent proficiency distribution.
b_i <- seq(-2, 2, length = n_items)
The generate_dich_data function uses mirt::simdata to simulate dichotomous data given the item discriminations ($a$), item difficulties ($b$), and sample size ($n$).
Note that the mirt package uses the slope-intercept parameterization. Therefore, the item difficulty parameters ($b$) must be transformed into the item intercepts $d_i = -a_i*b_i$. The transformation between the traditional IRT parameters (item discrimination and item difficulty) and the slope-intercept parameters can also be done with mirt::traditional2mirt.
# Simulate dichotomous item responses for n respondents to all items
# - 'a' denotes the item discriminations
# - 'b' denotes the item difficulties
# - 'n' denotes the sample size
generate_dich_data <- function(a, b, n) {
resp <-
mirt::simdata(a = a, d = -a*b, N = n, itemtype = "dich") %>%
as.data.frame()
return(resp)
}
II. Defining the test design and the process of missing values
4. Pattern of missingness (e.g., type of missingness, linking design)
5. Amount of missing data
The data_link_design function uses the complete simulated data to delete observations. Since there are two test versions in the study, each respondent is randomly assigned to test version A or test version B. Test version A contains the odd-numbered items and test version B contains the even-numbered items. Items 13 through 18 are present on both versions as linking items. Depending on the assigned test version, responses to items not included in the test version will have missing values.
# Induce missingness to the complete simulated data set
# - 'resp' denotes the complete data set
data_link_design <- function(resp) {
n <- nrow(resp)
n_items <- ncol(resp)
# Generate an indicator of the administered test version for each respondent
# assuming that about half of the sample receives each test version
resp$version <- sample(c(1, 2), n, replace = TRUE)
# Item responses not included in a test version are set to missing
# depending on the generated indicator of the administered test version.
resp[resp$version == 1, setdiff(seq(1, n_items), c(seq(1, n_items, 2), 13:18))] <- NA
resp[resp$version == 2, setdiff(seq(1, n_items), c(seq(2, n_items, 2), 13:18))] <- NA
resp <- subset(resp, select = -c(version))
return(resp)
}
III. Selecting the IRT model and the parameter of interest
6. Underlying IRT model (e.g., 1PL, 2PL)
7. IRT modeling software and estimation method
8. Parameters to extract
The estimate_irt function estimates the one-parametric IRT model (Rasch model) with mirt using the simulated data and returns a data.frame with the estimated item difficulties.
# Estimate item response model
# - 'resp' denotes the data set
estimate_irt <- function(resp) {
# Estimate a 1PL model using try-catch to handle errors
mod <- tryCatch(
mirt(data = resp, # Item responses
itemtype = 'Rasch', # 1PL model
verbose = FALSE),
error = function(e) NULL
)
# Extract item difficulties if model is estimated, else return NA
if (!is.null(mod)) {
est <- coef(mod, IRTpars = TRUE, simplify = TRUE)$items[, "b"]
} else {
est <- rep(NA, ncol(resp))
}
return(est)
}
IV. Setting up the Monte Carlo Simulation
9. Number of iterations
10. Sample sizes to evaluate
The Monte Carlo simulation runs n_iterations times, including the previous steps of (i) determining the data generation for the complete dataset, (ii) defining the test design and the process of missing values, (iii) selecting the IRT model and the parameter of interest.
Based on the estimated standard deviation of the MSE ($\sigma = 0.523$), a specified level of accuracy ($\delta = .05$), and a significance level ($\alpha = .05$), the required number of iterations was calculated as 438. Therefore, the simulation is run for different sample sizes between 100 and 600 (in increments of 50).
# Number of iterations
n_iterations <- 438
# Create data frame for results (res)
res <- data.frame()
# Check if result file already exists
if (file.exists("example_1_res.rds")) {
res <- readRDS("example_1_res.rds")
} else {
# Loop over different sample sizes (from 100 to 600, in steps of 100)
for (n_persons in seq(100, 600, 50)) {
# Nested loop, running 'n_iterations' times
for (iter in 1:n_iterations) {
dat <- generate_dich_data(a_i, b_i, n_persons) %>%
data_link_design()
res <- bind_rows(res,
data.frame(item = paste0("Item_", 1:length(b_i)),
iteration = iter,
n_persons = n_persons,
b_est = estimate_irt(dat),
b_true = b_i))
}
}
# Save the results
saveRDS(res, file = "example_1_res.rds")
}
Results
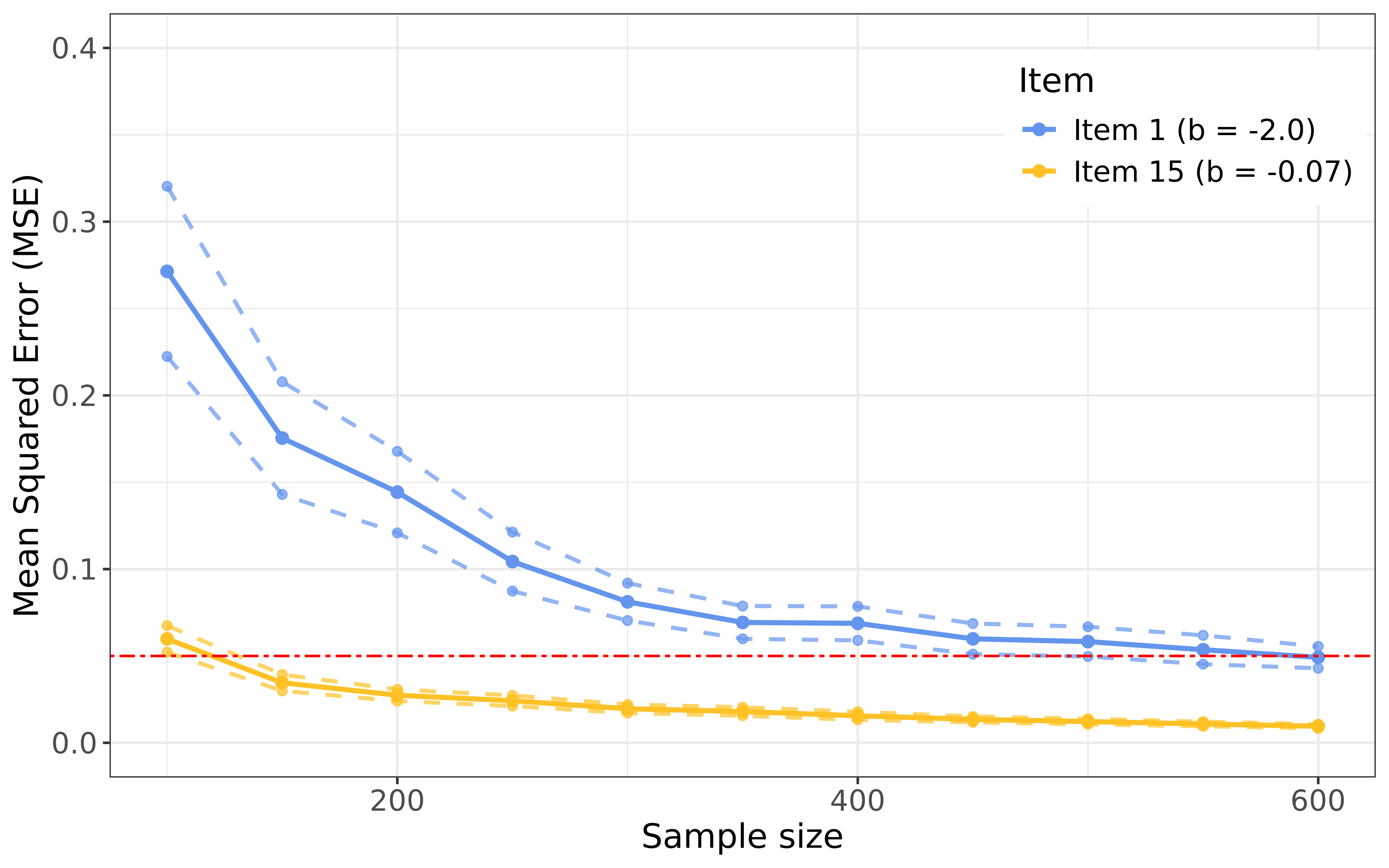
The figure shows the MSE and its 95% confidence interval (± 1.96 MCSE [Monte Carlo Standard Error]) for two items by sample size. For simplicity, only the results for items 1 and 15 are shown.
# Preparation and aggregation of results
res_plot <- res %>%
as_tibble() %>%
mutate(b_diff2 = (b_est - b_true)^2) %>%
group_by(item, n_persons) %>%
summarise(
MSE = mean(b_diff2, na.rm = TRUE), # Calculate the MSE for item difficulties
MCSE = sd(b_diff2, na.rm = TRUE) / sqrt(n() - 1), # Calculate the MCSE
.groups = 'drop') %>%
filter(item %in% c("Item_1", "Item_15")) %>% # Filter data for the 1st and 15th items
mutate(item = case_when(
item == "Item_1" ~ "Item 1 (b = -2.0)",
item == "Item_15" ~ "Item 15 (b = -0.07)"
))
# Plot mean squared error by sample size for item 1 and 15
ggplot(data=res_plot, aes(x=n_persons, color=item)) +
geom_line(aes(y = MSE), linewidth = 1, linetype = "solid") +
geom_point(aes(y = MSE), size = 2) +
# CI boundaries
geom_line(aes(y = MSE - 1.96 * MCSE), linewidth = 0.8, alpha = 0.7, linetype = "dashed") +
geom_point(aes(y = MSE - 1.96 * MCSE), size = 1.5, alpha = 0.7) +
geom_line(aes(y = MSE + 1.96 * MCSE), linewidth = 0.8, alpha = 0.7, linetype = "dashed") +
geom_point(aes(y = MSE + 1.96 * MCSE), size = 1.5, alpha = 0.7) +
geom_abline(intercept = .05, slope = 0, col="red", lty = "twodash") +
labs(
x = "Sample size",
y = "Mean Squared Error (MSE)",
color = "Item",
linetype = "Item"
) +
scale_color_manual(values = c("Item 1 (b = -2.0)" = "cornflowerblue",
"Item 15 (b = -0.07)" = "goldenrod1")) +
scale_linetype_manual(values = c("Item 1 (b = -2.0)" = "solid",
"Item 15 (b = -0.07)" = "solid")) +
ylim(0, 0.4) +
xlim(100, 600) +
theme_bw() +
theme(
axis.title = element_text(size = 14),
axis.text = element_text(size = 12),
legend.title = element_text(size = 14),
legend.text = element_text(size = 12),
legend.position = "inside",
legend.position.inside = c(.85, .85)
)
# Documentation for transparency and reproducibility
print(sessionInfo(), locale=FALSE)